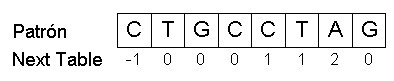ALGORITMO DE CORRESPONDENCIA EXACTA

Este algoritmo se basa en buscar patrones exactos dentro de una secuencia de DNA, por medio del algoritmo "tonto" de recorrer toda la secuencia nucleótido por nucleótido, haciendo la comparación oportuna con el patrón.El principal factor a tener en cuenta es el problema de encontrar todos los posibles desplazamientos a lo largo de la secuencia.

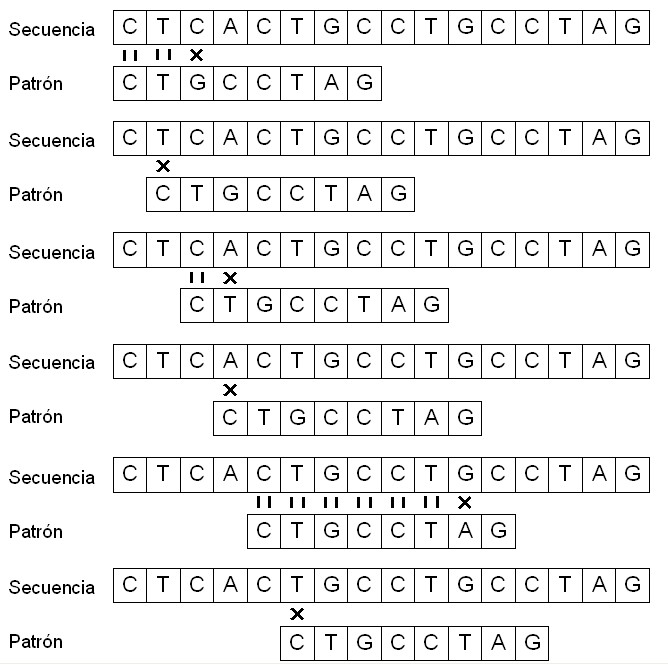
Por ejemplo, si consideramos una secuencia t = {CTCACTGCCTGCCTAG} y un patrón p = {CTGCCTAG}, el patrón p se encuentra dentro de t a partir del noveno símbolo, y podemos decir que el patrón p aparece en t con un desplazamiento s, en este caso, s = 8.

Esto hace que los símbolos:

sean exactamente los de p, es decir:

Así, podremos llegar a encontrar un máximo de n - m + 1 desplazamientos s.

Este algoritmo, también conocido como de "fuerza bruta", funciona de una manera simple y obvia: después de un mismatch entre patrón y secuencia, el proceso de comparación se detiene y se incia otra vez desplazando el patrón una posición sobre la secuencia. En el ejemplo, la comparación entre patrón y secuencia comienza en la primera posición de ambos. Como los símbolos son iguales, la comparación continúa con los dos nucleótidos siguientes, en los que también hay coincidencia. En este caso, la comparación también continúa con los dos nucleótidos siguientes pero no se produce coincidencia. Así pues, la comparación entre patrón y secuencia empieza otra vez, pero ahora se compara la posición 0 del vector con la posición 1 del vector secuencia (segundo nucleótido), i así se hace sucesivamente, desplazando el inicio de la comparación del patrón sobre la secuencia únicamente un nucleótido.

A la hora de construir la next table, se asigna un valor de -1 a la posición 0 del vector de la next table y un 0 a la posición 1. El valor -1 en la posición 0 es una señal cualquiera que nos sirve para comenzar la comparación con el siguiente nucleótido de la secuencia en caso que se produzca un mismatch entre la posición 0 del vector patrón y un símbolo de la secuencia. En la posición 1 del vector de la next table se tendría que comparar el prefijo de la posición 1, formado exclusivamente por la posición 0, con el patrón antes de la posición 1. Como el prefijo, aunque es coincidente, siempre será máximo, asignaremos directamente el valor 0 a la posición 1. Continuamos con la posición 2 del vector patrón, donde se mira el número máximo de nucleótidos coincidentes con el patrón antes de esa posición. En este caso es sencillo, ya que sólo hemos de mirar si la posición 1 (T) es igual que la posición 0 (C) del vector patró. Como no son iguales, el valor del vector de la next table para la posición 2 será 0. Si pasamos a la posición 3, hemos de comparar si el prefijo formado por las posiciones 1 i 2 o el formado únicamente por la 2 coinciden con el patrón des de su inicio, es decir, si el prefijo constituído por las posiciones 1 y 2 es igual a las posiciones 0 y 1 o si la posición 2 es igual que la posición 0 del patrón. En este caso, no se produce ninguna coincidencia, de manera que el valor de la next table para la posición 3 es 0. Si miramos la posición 4, tendremos que comparar los prefijos formados por las posiciones 1, 2 y 3, por las posiciones 2 i 3 o por la posición 3 con el patrón que les precede. Aquí vemos que la posición 3 es igual a la posición 0 del vector patrón, así que el valor del vector de la next table para la posición 4 es igual a 1 (el prefijo mayor en la posición 4 que coincide con el patrón está formado por un nucleótido). Si ahora nos centrado en la posición 5, ocurre lo mismo que con la posición 4, y el prefijo mayor que coincide con el patrón es de un nucleótido, de manera que el valor de la next table para la posición 5 es 1. Cuando miramos la posición 6, tenemos diferentes prefijos: los formados por las posiciones 1, 2, 3, 4 y 5, por 2, 3, 4 y 5, por 3, 4 y 5, por 4 y 5 y por 5. En este caso, el prefijo formado por las posiciones 4 y 5 coinciden con las posiciones 0 y 1 del vector patrón, y pondremos un 2 (2 nucleótidos coincidentes) en la posición 6 del vector de la next table. Para finalizar con la next table de este patrón, miramos la última posición, la 7. Ninguno de los prefijos para esta posición coincide con el patrón. Así pues, el vector de la next table tendrá un valor de 0 en la posición 7.

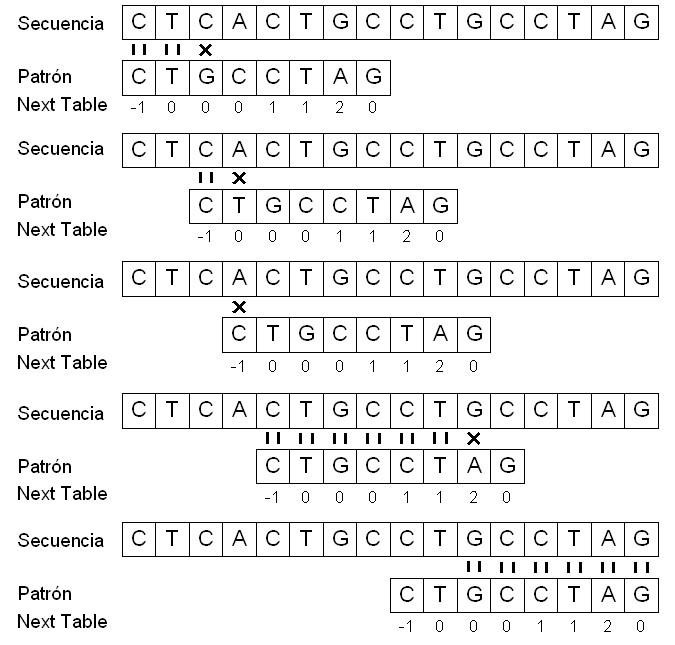
Una vez construída la next table, se procede a implementar el KMP. El funcionamiento de este seria el siguiente: siempre que hay una correspondencia entre dos símbolos (uno de la secuencia y el otro del patrón) se pasa a la siguiente posición, tanto de la secuencia como del patrón. En cambio, cuando tenemos dos símbolos diferentes, se empieza a buscar el patrón en la secuencia a partir de la posición del patrón que nos indica la next table.

Por ejemplo:
Los dos primeros nucleótidos de la secuencia son C y T y se corresponden con los dos primeros símbolos del patrón. Ahora bien, cuando llegamos al tercer nucleótido, en la secuencia encontramos una C y en el patrón una G. Con el algoritmo de Knuth-Morris-Pratt miramos el valor que tiene la next table para el tercer símbolo y vemos que es un 0. Ahora se comparará la posición 3 de la secuencia (donde se había producido el mismatch) con la posición 0 del patrón, que como es un vector, será la primera posición, la C. Con este paso nos hemos ahorrado la comparación del patrón con la segunda posición de la secuencia, porque al disponer de la next table (que actúa como un sistema de memoria) ya sabemos qeu esta comparación es inecesaria porque no puede puede dar lugar a una correspondencia exacta con el patrón.

En la penúltima comparación del patrón con la secuencia, en que el patrón empieza a comparar con el nucleótido 5 de la secuencia, se produce una correspondencia entre los símbolos hasta llegar al nucleótido número 11 de la secuencia, donde hay una G, que se compara con la A del patrón. Como se produce este mismatch, miramos el valor de esta A en la next table y observamos un 2. Entonces, se empieza a comparar el símbolo el símbolo G de la secuencia con el de la posición 2 del vector patrón. Finalmente, encontramos el patrón p dentro de la secuencia t con un desplazamiento s igual a 8.

Una vez implementado el algoritmo de Knuth-Morris-Pratt en lenguaje de programación Perl para la búsqueda de subsecuencias únicas en el genoma humano de los genes GH, IGF-1 y EPO, se determinó que el tiempo de ejecución del programa sería de unos 40* días aproximadamente para cada gen, en el mejor de los casos. Este tiempo es muy superior a los antecendentes de que disponíamos por parte del supervisor del trabajo, el Dr. Robert Castelo, que ya había implementado el algoritmo simple de correspondencia exacta en lenguaje C con la finalidad de encontrar patrones únicos del gen de la EPO de ratón en el genoma de este organismo. En un principio, se había pensado que implementando el algoritmo de Knuth-Morris-Pratt, que es más eficiente que el algoritmo simple de correspondencia exacta, habría una ganancia computacional, aunque el lenguaje Perl es más lento que el lenguaje C. Pero la gran diferencia en términos de tiempo entre estos dos lenguajes de programación ha hecho imposible obtener las subsecuencias únicas de los genes de interés en el periodo establecido. No obstante, hemos creado un programa basado en la implementación del algoritmo de Knuth-Morris-Pratt que es capaz de realizar esta búsqueda de patrones únicos en todo el genoma dado un mRNA. Para la comprobación del correcto funcionamiento del programa hemos corroborado los resultados obtenidos por el Dr. Robert Castelo, es decir, comprobar que los tres patrones únicos encontrados en el gen de la EPO de ratón son subsecuencias únicas del cromosoma 5 del genoma de ratón, donde se encuentra el locus de este gen.

* El cálculo de estos 40 días aproximados se llevó a cabo de la siguiente forma:
Nuestro programa contenia una serie de "chivatos" que nos informaban del estado de ejecución del mismo a cada momento: la longitud a la que buscaba, el patrón que comprobaba y en qué cromosoma, y dentro de cada cromosoma, cada vez que ya había realizado unas 50.000 línias. Mediante estos "prints" a la ventana terminal pudimos detectar que, en uno de los ordenadores más rápidos que el Dr. Robert Castelo nos permitió acceder, el programa procesaba unas 50.000 línias cada 5 segundos. Teniendo en cuenta que el genoma de ratón tiene un total de 63.299.105 línias, el programa tardaría unas 6.329,91 segundos a procesar todo el genoma para cada patrón. Como una hora son 3.600 segundos, esto serían 1,75 horas. Si para el mRNA de la EPO de Mus musculus, que tiene 579 nucleótidos, el programa nos genera unos 566 patrones de 14 nucleótidos, el número total de horas necesarias para ejecutarlo es de 990,5 horas, que equivalen a unos 41 días aproximadamente.

Tal como hemos comentado en el apartado de objetivos, para poder monitorizar la expresión génica del mRNA en el caso de un posible dopaje genético, hace falta disponer de secuencias específicamente marcadas y que sean capaces de hibridar selectivamente con el mRNA diana. Por este motivo, interesa obtener unos patrones únicos de los genes de interés (GH, IGF-1 y EPO) que sean accesibles a los PNAs marcados y no estén escondidos en la estructura secundaria del mRNA. Así pues, una vez obtenidos los patrones únicos en el genoma (concretamente en el cromosoma 5 del genoma de ratón) a través de la implementación del algoritmo de Knuth-Morris-Pratt, se predice la estructura secundaria del mRNA y la localización de las las subsecuencias encontradas del gen de la EPO con el programa mFOLD. Este programa, creado por el Dr. Michael Zuker del Rensselaer Polytechnic Institute's School of Science y disponible como servicio web, es un software que predice el plegamiento y la estructura secundaria tanto de RNA como de DNA.

La metodología seguida en este proyecto es la siguiente:

1. Implementación del algoritmo simple de correspondencia exacta de secuencias para la búsqueda de patrones únicos en un mRNA.
2. Implementación del algoritmo de Knuth-Morris-Pratt de la correspondencia exacta de secuencias para la búsqueda de patrones únicos en un mRNA que también sean únicos en todo el genoma.
3. Cálculo del número de comparaciones de nucleótidos que hacen ambos algoritmos para encontrar los patrones únicos de cada mRNA dentro de su propio mRNA.
4. Utilizando la implementación del algoritmo de Knuth-Morris-Pratt, buscar si las subsecuencias únicas de 14 nucleoótidos (CGACAGTCGAGTTC, AGTGGTCTACGTAG y GGGTCTACGCCAAC), encontradas por el Dr. Robert Castelo en el gen de la EPO de ratón son únicas en el cromosoma 5 de este organismo.
5. Localizar estas subsecuencias únicas en la estructura secundaria del mRNA de la EPO de ratón para determinar si se encuentran en las regiones más internas o en las más expuestas.

Las secuencias utilizadas para la elaboración de este proyecto, obtenidas en la base de datos de NCBI, son las siguientes: