| Introducció | Objectius | Metodologia | Programes | Resultats | Conclusions | Referències | Autores | Agraïments |
METODOLOGIA
Per tal de dur a terme el projecte i abordar el problema de la correspondència exacta entre símbols, hem hagut d'implementar dos algorismes: l'algorisme simple de correspondència exacta i l'algorisme de Knuth-Morris-Pratt. Aquest algorisme es basa en buscar patrons exactes dins d'un seqüència de DNA, per mitjà de l'algorisme "tonto" de recórrer tota la seqüència nucleòtid per nucleòtid, fent la comparació oportuna amb el patró. El principal factor a tenir en compte és el problema de trobar tots els possibles desplaçaments al llarg de la seqüència.
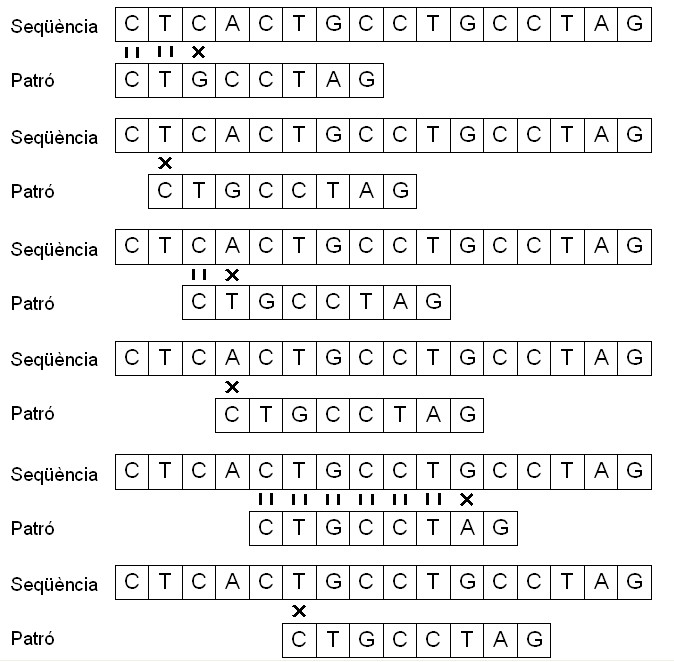
Per exemple, si considerem una seqüència t = {CTCACTGCCTGCCTAG} i un patró p = {CTGCCTAG}, el patró p es troba dins de t a partir del novè símbol, i podem dir que el patró p apareix en t amb desplaçament s, en aquest cas, s = 8.
Això fa que els símbols:
|
||||||||||||||
|
t[s+1]t[s+2]t[s+3]...t[s+m] |
||||||||||||||
siguin exactament els de p, és a dir: |
||||||||||||||
t[s+1] == p[0] t[s+2] == p[1] t[s+3] == p[2] ... t[s+m] == p[m-1] |
||||||||||||||
Així, podrem arribar a trobar com a màxim n - m + 1 desplaçaments s.
Aquest algorisme, també conegut com de "força bruta", funciona d'una manera simple i òbvia: després d'un mismatch entre patró i seqüència, el procés de comparació s'atura i s'inicïa un altre cop desplaçant el patró una posició sobre la seqüència. En l'exemple, la comparació entre patró i seqüència comença amb la primera posició de tots dos. Com que els símbols són iguals, la comparació continua amb els dos nucleòtids següents, en els quals també hi ha coincidència. En aquest cas, la comparació també continua amb els dos nucleòtids següents però no es produeix coincidència. Així doncs, la comparació entre patró i seqüència comença un altre cop, però ara es compara la posició 0 del vector patró amb la posició 1 del vector seqüència (segon nucleòtid), i així es fa successivament, desplaçant l'inici de la comparació del patró sobre la seqüència només un nucleòtid.
|
||||||||||||||
|
||||||||||||||
Com a resultat, trobem que la seqüència t conté el patró p amb un desplaçament s igual a 8.
|
||||||||||||||
|
||||||||||||||
|
|
||||||||||||||
 ALGORISME DE KNUTH-MORRIS-PRATT ALGORISME DE KNUTH-MORRIS-PRATT
L'algorisme de Knuth-Morris-Pratt (KMP) és un algorisme linial per a la cerca exacta de patrons. És semblant a l'algorisme simple de correspondència exacta però la principal diferència és que el KMP es basa en el fet que, després de trobar el primer símbol que no coincideix entre el patró i la seqüència, nosaltres ja coneixem els símbols del patró que hem comparat fins aquell punt. D'aquesta manera, s'aconsegueix que després d'un aparellament incorrecte el procés no continuï (des de l'inici del patró) amb el següent caràcter de la seqüència, i així no haver de comparar posicions que ja se sap prèviament que no donaran lloc a una ocurrència exacta del patró.
El KMP es beneficia de la informació que el propi patró conté ja que es desconeix la seqüència on es fa la cerca. Per aprofitar aquest fet, cal construir una taula de desplaçaments coincidents dins del patró abans de començar la cerca. Aquesta taula, anomenada "next table", té una posició per a cada posició del patró, i a cada posició n s'introduirà el nombre màxim de símbols coincidents amb el patró abans d'aquella posició (sense coincidir el prefix sencer de n símbols).És a dir, a cada posició n es comproven les coincidències existents entre els diferents prefixos de n i el patró que precedeix a n.
Continuant amb l'exemple anterior en què teníem una seqüència t ={CTCACTGCCTGCCTAG} i un patró p= {CTGCCTAG}, el patró p es troba dins de t a partir del novè símbol. Llavors, com abans, podem dir que el patró p es troba a t amb un desplaçament s = 8.
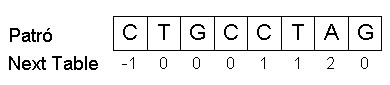
En el KMP, primer de tot es calcula la next table del patró. Pel patró p = {CTGCCTAG} seria la següent:
|
||||||||||||||
|
||||||||||||||
A l'hora de construir la next table, s'assigna un valor de -1 a la posició 0 del vector de la next table i un 0 a la posició 1. El valor -1 a la posició 0 és un senyal qualsevol que ens serveix per començar la comparació amb el següent nucleòtid de la seqüència en el cas que es produeixi un mismatch entre la posició 0 del patró i un símbol de la seqüència. En la posició 1 del vector de la next table s'hauria de comparar el prefix de la posició 1, format exclusivament per la posició 0, amb el patró abans de la posició 1. Com que el prefix, tot i ser coincident, sempre serà màxim, assignarem directament el valor de 0 a la posició 1. Continuem amb la posició 2 del vector patró, on es mira el nombre de nucleòtids coincidents amb el patró abans d'aquella posició. En aquest cas és senzill, ja que només hem de mirar si la posició 1 (T) és igual que la posició 0 (C) del vector patró. Com que no són iguals, el valor del vector de la next table per la posició 2 serà 0. Si passem a la posició 3, hem de comparar si el prefix format per les posicions 1 i 2 o el format únicament per la 2 coindeixen amb el patró des del seu inici, és a dir, si el prefix constituït per les posicions 1 i 2 és igual a les posicions 0 i 1 o si la posició 2 és igual que la posició 0 del patró. En aquest cas, tampoc hi ha cap coincidència, de manera que el valor de la next table per la posició 3 és 0. Si mirem la posició 4, haurem de comparar els prefixos formats per les posicions 1, 2 i 3, per les posicions 2 i 3 o per la posició 3 amb el patró que els precedeix. Aquí veiem que la posició 3 és igual a la posició 0 del vector patró, així que el valor del vector de la next table per la posició 4 és igual a 1 (el prefix més gran a la posició 4 que coincideix amb el patró està format per un nucleòtid). Si ara ens centrem en la posició 5, passa el mateix que amb la posició 4, i el prefix més gran que coincideix amb el patró és d'un nucleòtid, de manera que el valor de la next table per la posició 5 és 1. Quan mirem la posició 6, tenim diferents prefixos: els formats per les posicions 1, 2, 3, 4 i 5, per 2, 3, 4, i 5, per 3, 4 i 5, per 4 i 5 i per 5. En aquest cas, el prefix format per les posicions 4 i 5 coincideix amb les posicions 0 i 1 del vector patró, i posarem un 2 (2 nucleòtids coincidents) a la posició 6 del vector de la next table. Per finalitzar amb la next table d'aquest patró, mirem l'última posició, la 7. Cap dels prefixos per aquesta posició coincideix amb el patró. Així doncs, el vector de la next table tindrà un valor de 0 a la posició 7.
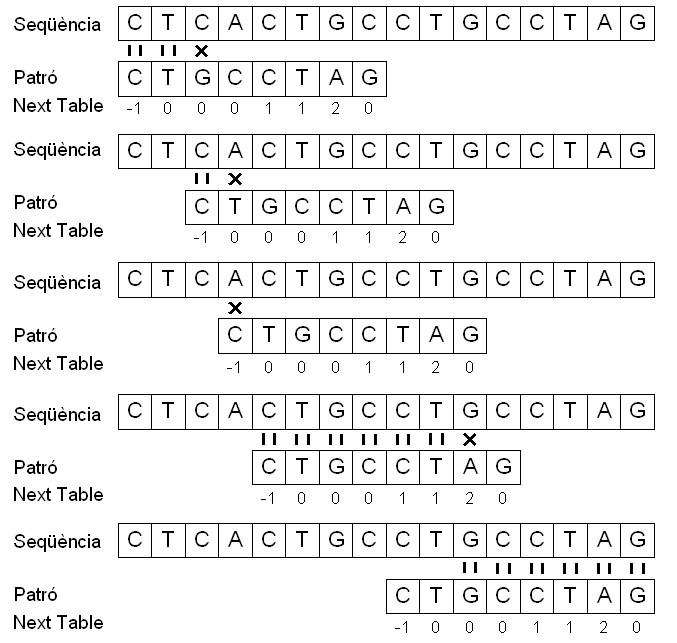
Un cop construïda la next table, es procedeix a implementar el KMP. El funcionament d'aquest seria el següent: sempre que hi ha correspondència entre dos símbols (un de la seqüència i l'altre del patró) es passa a la posició següent, tant de la seqüència com del patró. En canvi, quan tenim dos símbol diferents, es comença a buscar el patró a la seqüència a partir de la posició del patró que ens indica la next table.
Per exemple:
En la penúltima comparació del patró amb la seqüència, en què el patró comença a comparar amb el nucleòtid 5 de la seqüència, es produeix una correspondència entre els símbols fins arribar al nucleòtid número 11 de la seqüència, on hi ha una G, que es compara amb la A del patró. Com que hi ha aquest mismatch, mirem el valor d'aquesta A a la next table i observem un 2. Aleshores, es comença a comparar el símbol G de la seqüència amb el de la posició 2 del vector patró. Finalment, trobem el patró p dins la seqüència t amb un desplaçament s igual a 8.
|
||||||||||||||
|
||||||||||||||
|
|
Una vegada implementat l'algorisme de Knuth-Morris-Pratt en llenguatge de programació Perl per a la cerca de subseqüències úniques en el genoma humà del gens GH, IGF-1 i EPO, es va determinar que el temps d'execució del programa seria d'uns 40* dies aproximadament per a cada gen, en el millor dels casos. Aquest temps és molt superior als antecedents de què disposavem per part del supervisor del treball, el Dr. Robert Castelo, que ja havia implementat l'algorisme simple de correspondència exacta en llenguatge C amb la finalitat de trobar patrons únics del gen de la EPO de ratolí en el genoma d'aquest organisme. En un principi, s'havia pensat que implementant l'algorisme de Knuth-Morris-Pratt, que és més eficient que l'algorisme simple de correspondència exacta, hi hauria un guany computacional, tot i que el llenguatge Perl és més lent que el llenguatge C. Però, la gran diferència en termes de temps entre aquests dos llenguatges de programació ha fet impossible obtenir les subseqüències úniques dels gens d'interès en els terminis establerts. No obstant, hem creat un programa basat en la implementació de l'algorisme de Knuth-Morris-Pratt que és capaç de realitzar aquesta cerca de patrons únics en tot el genoma donat un mRNA. Per a la comprovació del correcte fucionament del programa hem corroborat els resultats obtinguts pel Dr. Robert Castelo, és a dir, comprovar que els tres patrons únics trobats al gen de la EPO de ratolí són subseqüències úniques del cromosoma 5 del genoma de ratolí, on es troba el locus d'aquest gen.
* El càlcul d'aquests 40 dies aproximats es va dur a terme de la següent manera:
|
|||||||||||||
|
|
||||||||||||||
Tal com hem comentat a l'apartat d'objectius, per poder monitoritzar l'expressió gènica del mRNA en el cas d'un possible dopatge genètic, cal disposar de seqüències específicament marcades i que siguin capaces d'hibridar selectivament amb el mRNA diana. Per aquest motiu, interessa obtenir uns patrons únics dels gens d'interès (GH, IGF-1 i EPO) que siguin accessibles als PNAs marcats i no estiguin amagats a l'estructura secundària del mRNA. Així doncs, un cop obtinguts els patrons únics al genoma (concretament en el cromosoma 5 del genoma de ratolí) a través de la implementació de l'algorisme de Knuth-Morris-Pratt, es prediu l'estructura secundària del mRNA i la localització de les subseqüències trobades del gen de la EPO amb el programa mFOLD. Aquest programa, creat pel Dr. Michael Zuker del Rensselaer Polytechnic Institute's School of Science i disponible com a servei web, és un software que prediu el plegament i l'estructura secundària tant de RNA com de DNA |
||||||||||||||
|
|
||||||||||||||
La metodologia seguida en aquest projecte és la següent:
|
||||||||||||||
|
|
||||||||||||||
Les seqüències utilitzades per a l'elaboració d'aquest projecte, obtingudes a la base de dades de NCBI, són les següents: |
||||||||||||||
|