DISSENY DEL PROGRAMA
Aquest programa (com molts altres) està estructurat en quatre blocs bàsics. És important destacar que, enfront el plantejament inicial, s'han fet diverses millores, de les quals es recomana la seva lectura abans d'accedir a les explicacions dels blocs esmentats:
Si voleu fer un anàlisi més exhaustiu sobre el disseny de Let's seXXXqs!!!, podeu veure el seu Codi font; aquest, disposa d'anotacions al costat de cada comanda i resulta molt autoexplicatiu.
La principal millora que s'ha fet respecte al plantejament inicial és la d'aplicar l'anomenat Affine Gap Model. Si ens fixem en els següents alineaments:
MILLORES
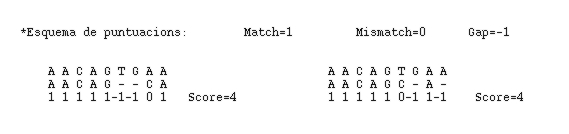
...veurem que tenen la mateixa puntuació final i per tant tots dos podrien ser considerats com a òptims, però el primer té més sentit des del punt de vista evolutiu, doncs només presenta un fenòmen d'inserció o deleció, mentres el segon en necessita dos. Aquesta distinció ens serà possible gràcies a l'Affine Gap Model, doncs la penalització de salt es desdoblarà en dos components:
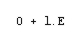
... on O és l'obertura de salt i E l'extensió de salt, multiplicat per l posicions seguides (en les que s'ha extés el salt). Així, el nostre exemple anterior quedaria de la següent manera:

Per aplicar aquest model al nostre programa l'opció més intuitiva és la d'afegir una iteració al programa dins de l'algorisme, de manera que calculi la màxima puntuació d'introduir un salt entre totes les possibilitats que ofereixen totes les caselles anteriors de la fila (o columna, segons quina seqüència sigui) i no només la de la casella anterior. El problema d'aquesta solució és que fa augmentar l'ordre de complexitat de l'algorisme de cuadràtic a cúbic!!!
La segona millora (dins de la primera...) és precisament la de poder aplicar l'Affine Gap Model mantenint l'ordre de complexitat cuadràtic, mitjançant el següent algorisme:
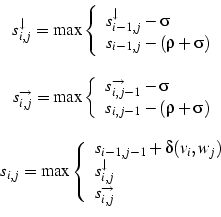
Aquest, és una adaptació del que ja hem vist anteriorment a l'apartat Mètodes (programació dinàmica). En aquest, en comptes d'escollir entre les tres opcions ja esmentades, s'escull entre l'opció de sumar la puntuació d'alinear els dos símbols a la de la casella anterior en diagonal i les opcions dels valors de les caselles Si,j de les matrius de salts. Aquestes dues matrius "noves" es generen paral.lela, però prèviament (referent a cada casella Si,j) a la de puntuacions, així ja existeix un valor per quan l'algorisme recorre a elles a l'hora de triar entre les tres opcions abans esmentades. El sentit d'aquestes matrius, és que abans de triar si introduim salt o no, haurem de triar si és millor que aquest sigui nou (per tant obertura de salt) o que sigui l'extensió d'un d'anterior.
*(Per entendre millor el funcionament d'aquest procés, podeu visitar l'apartat Exemples de la plana web)
La tercera millora és que no s'ha considerat obertura de salt en aquells salts situats al principi de la seqüència, doncs a nivell biològic és més provable que no pas un salt enmig, doncs el primer pot provenir d'un salt ja obert en la part anterior de la seqüència (que no coneixem o que no estem alineant...), en canvi, en el segon cas sabem del cert que el salt s'està obrint. Per tant, en la primera casella de la primera fila i la primera casella de la primera columna de la matriu de puntuacions, es penalitza només amb l'extensió de salt.
Finalment comentar que, degut al caracter seqüencial de l'aplicació de l'algorisme, hi haurà preferències en cas d'empat en les puntuacions a l'hora de triar les diverses opcions. En el nostre cas, es dóna preferència a l'extensió de salt enfront l'obertura de salt, i a l'introducció d'un salt a la segona i primera seqüència (per aquest ordre) enfront l'alineament dels respectius símbols.
DECLARACIÓ DE VARIABLES
En aquest bloc senzillament es llisten les variables més importants que farem servir durant la consecució del programa. Això ho fem perquè el programa necessita que si hem d'utilitzar variables prèviament les declarem, o sigui, que especifiquem la intenció d'utilitzar-les. Posteriorment ja les inicialitzarem assignant-les un/s valor/s per primer cop.
ENTRADA DE DADES
En aquest bloc es realitzen les següents accions:
COS DEL PROGRAMA
Aquest bloc és el més important; el podríem descriure com el "motor" del programa. En ell es realitzen les següents accions:
SORTIDA DE DADES
Aquest bloc és el que s'ocuparà de retornar-nos els resultats que esperem després d'haver executat el programa; senzillament fa:
FUNCIONS
En aquest bloc tenim totes les funcions necessàries per a executar el programa. Si us mireu el Codi font, veureu que és on realment s'hi troben totes les comandes... Les funcions per a executar Let's seXXqs!!! són (en ordre d'aparició):