EXEMPLE DIDÀCTIC
 |
Què passa si intentem alinear una proteïna humana amb una de porc llanut??? Per saber quin futur espera als protagonistes de la nostra foto, a continuació realitzarem l'alineament entre dues seqüències curtes per poder mostrar les matrius que es generen. Així veurem com es construeixen i podrem seguir pas a pas el procés que realitza Let's seXXXqs!!! per trobar l'alineament òptim. Utilitzarem les següents seqüències: >humà muntador aagtgaca >porc llanut acgaca |
Per als càlculs de les puntuacions, farem servir una penalització per obertura de salt de -2, una per extensió de salt de -1 (visita l'apartat Disseny (millores) si encara no ho has fet, per a entendre bé l'Affine Gap Model), i la següent matriu de puntuacions entre nucleòtids (s'ha triat DNA per a fer els càlculs més senzills i ràpids):

Primer de tot, ens familiaritzarem amb la matriu "base" que farem servir; aquesta, "enfronta" les dues seqüències de manera que la primera la situarem en la dimensió vertical (files, i) i la segona a l'horitzontal (columnes, j). La matriu té una fila i una columna "extres" per a poder introduir salts al principi de les seqüències. Cada casella i,j ens indicarà que estem a l'alineament parcial fins al símbol en la posició i de la primera seqüència i el de la posició j de la segona seqüència (excepte en les matrius de gaps...):

Com ja hem vist a l'apartat del Disseny del programa (es recomana la seva visita en profunditat, si encara no ho has fet, abans de seguir en aquest apartat...), treballarem amb quatre matrius diferents:
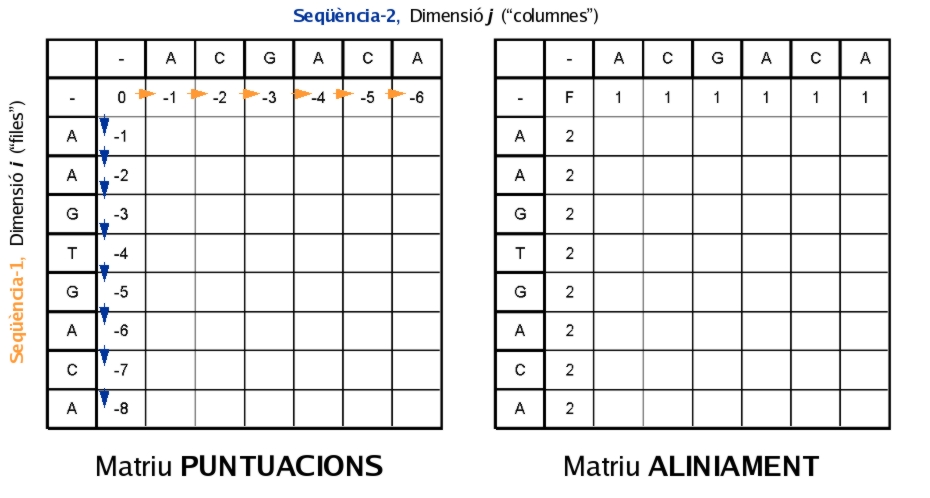
Donat que l'algorisme és una recurrència a caselles anteriors, haurem "d'inicialitzar" les diferents matrius per poder començar. Així, a la matriu de puntuacions posarem un 0 a la primera casella (puntuació inicial) i després anirem "arrossegant" la penalització per extensió de salt per tota la primera fila (salts a la primera seqüència) i la primera columna (salts a la segona seqüència); *no penalitzem l'obertura del salt perquè ens trobem als començaments de les seqüències (ja explicat a Disseny (millores)...). Paral.lelament posarem una "F" a la primera casella de la matriu d'alineament (que indicarà al programa que ja ha acabat de remuntar l'alineament òptim), i reflectirem també el procés d'arrossegar el salt a la primera fila i columna amb les notacions "1" i "2", que indiquen que s'ha introduït salt a la seqüència 1 i 2 respectivament:
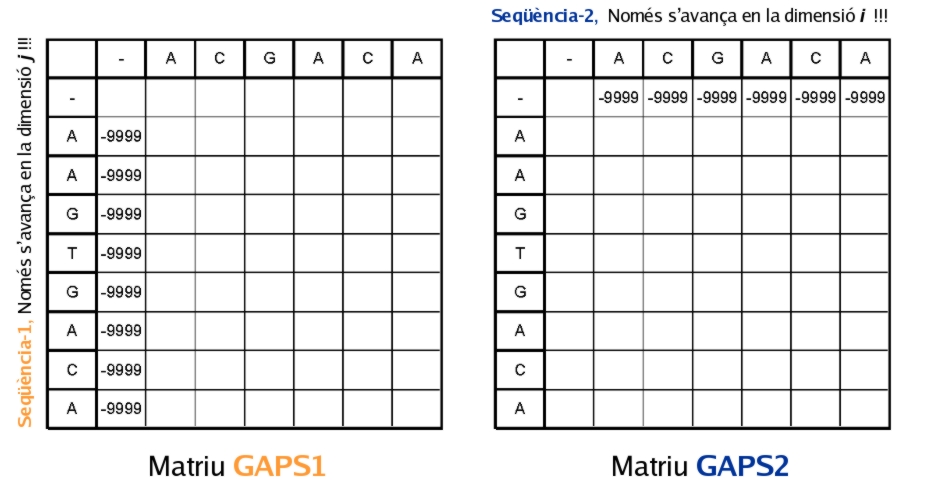
Les matrius de gaps són una mica més particulars... Com que fan referència a una sola seqüència, només "avancen" en una direcció; això vol dir que per al càlcul de les seves caselles, l'algorisme només fa la recurrència sobre les caselles anteriors en la mateixa dimensió. Així, per a la matriu referent a la primera seqüència, s'avança de forma horitzontal, i en la referent a la segona, de forma vertical.
Per a inicialitzar-la, posarem un valor molt negatiu a la primera columna (o fila, respectivament) per a restringir la primera elecció de l'algorisme; això ho fem perquè si no, la màxima puntuació de la segona columna (o fila, respectivament) provindria erròniament d'extendre un salt que encara no s'ha obert (ni s'ha penalitzat com a obert). També cal destacar que la primera fila (o columna, respectivament) estarà buida, doncs no es recorre a cap de les seves caselles:
Ara que les matrius ja estan inicialitzades, ja podem passar a omplir-les mitjançant l'algorisme de programació dinàmica. A partir d'ara cal fixar-se en l'algorisme, la matriu de similituds emprada i les penalitzacions de salt escollides. Si recordem l'aspecte que fa la millora de l'algorisme, per a poder penalitzar de forma diferent l'obertura de salts nous envers la de l'extensió d'anteriors:
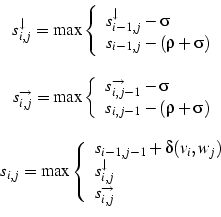
...veurem que abans de triar quina de les tres opcions és la que aporta la puntuació màxima (entre alinear els dos símbols, introduir salt a la primera seqüència, o a la segona), hem de triar el tipus de salt a introduir. Per exemple, en el nostre cas per a la primera casella a omplir de la matriu "GAPS1" el càlcul seria triar entre:
Per tant, per a aquesta casella triarem l'obertura d'un salt nou. Per a l'altra matriu i la següent casella, farem el mateix:

Ara ja podem passar a omplir la casella corresponent a aquesta mateixa posició a la matriu de puntuacions i, conseqüentment, a la d'alineament. Per tant, haurem de triar entre:
Per tant, per a aquesta casella (i, en el nostre cas, també per a la casella següent...) triarem l'alineament dels símbols corresponents a les posicions i i j de les respectives seqüències. Paral.lelament ho anotarem a la matriu d'alineament amb una "P":
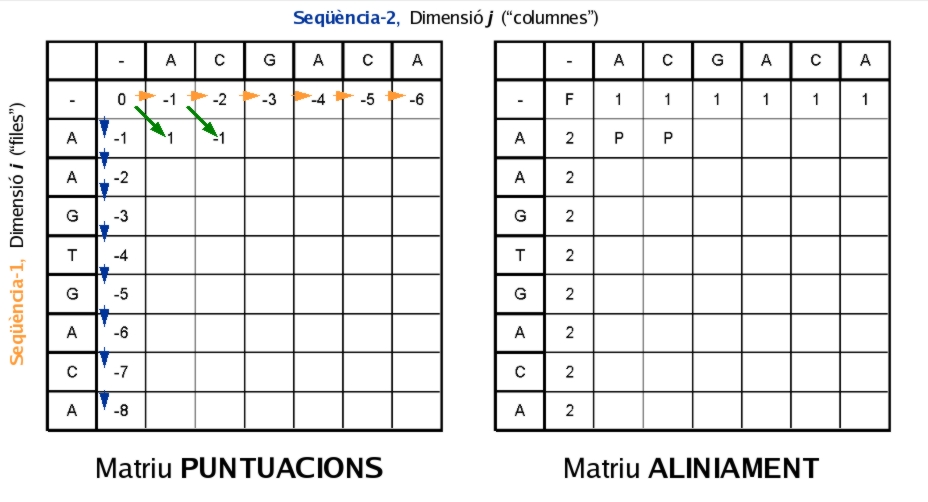
Si continuem amb aquesta mecànica per tota la fila, i després passem successivament a les següents files, acabarem d'omplir les matrius:
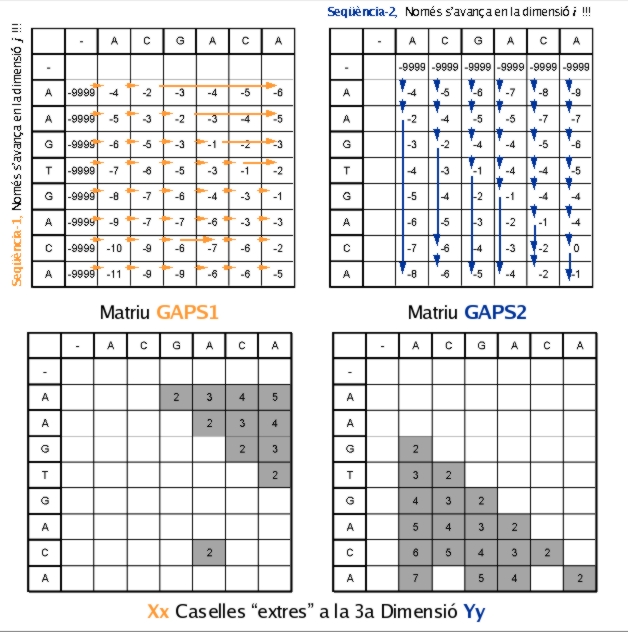
(Cal destacar que el programa crea unes caselles en la tercera dimensió de les matrius de gaps per a aquelles caselles que ho requereixin, o sigui, en les que s'ha triat penalització per extensió de salt. En aquestes s'hi assigna un valor numèric que indica la llargada del salt extès. Aquesta notació "extra" és necessària per a que posteriorment el programa sàpiga fins a quina casella ha de saltar per seguir remuntant l'alineament.)
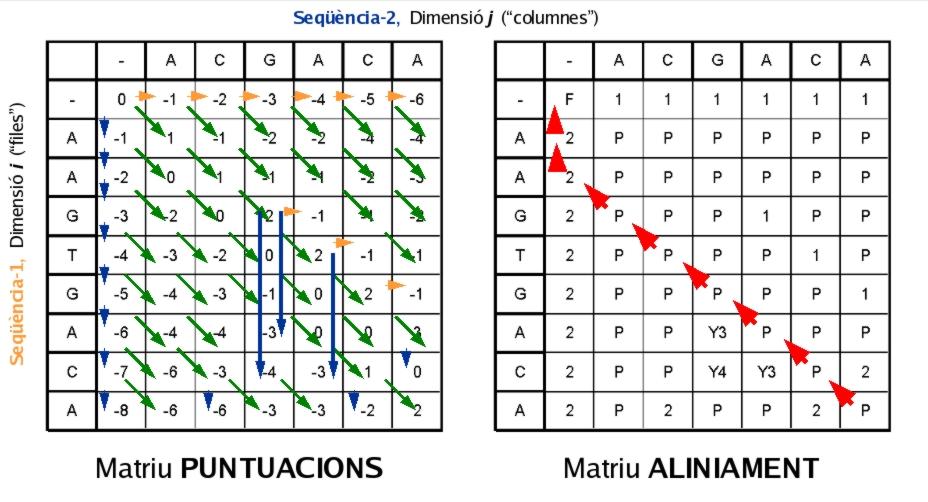
Un cop tenim les matrius omplertes, ja podem saber quin és l'alineament òptim i la seva puntuació. L'última casella (la de la cantonada d'abaix a la dreta) de la matriu de puntuacions ens indica la puntuació final o score (en aquest cas és 2); mentres, la de la matriu d'alineament ens indicarà successivament d'on prové l'alineament, i anirem remuntant fins a la casella "F". Llavors ja podrem reconstruir l'alineament, doncs a cada pas veurem si alineem, inserim salt, quina llargada té el salt, a quina seqüència s'introdueix... Per exemple, la notació "X2" indicaria que hem de remuntar horitzontalment dues caselles, i la "Y4" que ho hem de fer verticalment quatre caselles. Així doncs, aquests és l'alineament òptim entre les dues seqüències:
Finalment, per corroborar que aquests dos animalots alineen prou bé i comprovar així que ho haguem fet correctament, ho contrastem amb el resultat que ens mostra el programa:
