Identificació computacional de llocs d'unió a factors de transcripció

Les següents instruccions us han de servir per desenvolupar un programa en Perl al qual li doneu un fitxer amb matrius de factors de transcripció (FTs) i un altre fitxer amb una seqüència d'una regió promotora en format FASTA i el programa mostra la llista dels FTs proporcionats amb un p-value per cada FT que ens indiqui la probabilitat de rebutjar erròniament la hipòtesi inicial de que el factor no s'uneix.

Com a conjunt de matrius de FTs fareu anar el que trobareu dins el fitxer humanfactors_selectedmatrices.txt que conté matrius de 13 FTs humans diferents extretes del conjunt de matrius de FTs que fa anar el programa PROMO. El programa, per tant, l'hauriem de poder cridar des del shell d'aquesta forma:

$ ./identificacio_de_lufs.pl humanfactors_selectedmatrices.txt sequenciapromotora.fa

Desenvolupeu el programa seguint els següents passos:

comenceu fent que el programa llegeixi el fitxer de matrius, matriu a matriu, enregistrant-la en memoria com a un hash de vectors. Per comprovar que el programa llegeix i emmagatzema be les matrius, feu que us mostri per pantalla el contingut del hash de vectors un cop l'heu omplert.
Cada matriu en el fitxer de matrius segueix el següent format:
```
    FA  AP-1 [T00029]
    XX
    P0	A	C	G	T
    00	3	0	7	28
    01	4	1	31	2
    02	38	0	0	0
    03	0	0	38	0
    04	0	0	0	38
    05	0	38	0	0
    06	38	0	0	0
    //
    
```
on la primera columna de texte determina el tipus d'informació emmagatzemada a la línia de la següent forma:
- FA nom del FT i número d'accés a la base de dades de FTs TRANSFAC.
- XX línia separadora que marca el començament de la matriu en sí mateixa.
- P0 encapçalament de la matriu indicant a quin nucleòtid està associat cada columna de les línies següents.
- 00 occurrències de cada nuclòtid a la primera posició del motiu.
- 01 occurrències de cada nuclòtid a la segona posició del motiu.
- nn occurrències de cada nuclòtid a la nn-èssima posició del motiu.
- // darrera línia de la informació relativa a la matriu.
per a cada FT heu de transformar la seva matriu d'ocurrències de nucleòtids en una matriu de pesos (popularment coneguda en anglès com a position weight matrix) de forma que obteniu una matriu on cada nucleòtid té associat un pes a cada posició diferent del motiu. Si denotem aquest pes per w_i(x) per indicar el pes associat al nucleòtid x a la posició i-èssima dins un motiu que anomenarem M, el seu càlcul el farem de la següent forma:
w_i(x) = log(p_i^M(x)) - log(p^B(x)),

on p_i^M(x) és la proporció d'ocurrències del nucleòtid x a la posició i del motiu M, i p^B(x) és la proporció d'ocurrències del nucleòtid x al llarg de tota la seqüència promotora, es a dir, la proporció de vegades que esperem observar el nucleòtid x a l'atzar dins aquesta seqüència. En el cas de que p_i^M(x) sigui 0 eviteu fer el càlcul del seu logaritme i considereu en el seu lloc un valor negatiu molt alt, com ara -999.
per a cada FT heu de calcular la puntuació que proporciona la seva matriu de pesos a cada possible posició d'unió del FT dins la seqüència promotora. Es a dir, per una seqüència promotora de llargada N i un FT que s'uneix a f nucleòtids, on per tant la matriu de pesos te f posicions, hi ha N-f+1 llocs d'unió possibles cadascun dels quals el puntuarem desplaçant una finestra de longitut f al llarg de la seqüència:

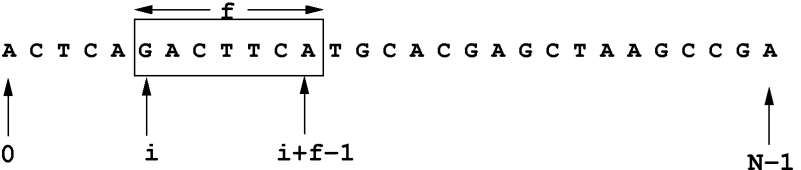
si denotem per s_i^M(x) la puntuació (en anglès score) que obtenim per al lloc d'unió que comença a la posició i dins una seqüència de nucleòtids x utilitzant una matriu de pesos associada al un motiu M, farem el seu càlcul de la següent forma:
s_i^M(x)=Σ_j=i^i+f-1 w_j(x_j),

on x_j denota el nucleòtid j-èssim dins la seqüència x. Enregistreu la puntuació màxima que obteniu al llarg de la seqüència així com la posició del lloc d'unió que la proporciona. Denotem en aquest document la puntuació màxima observada en la seqüència promotora amb s^*.
finalment, per cada FT, després del càlcul anterior cal estimar la freqüència amb la qual s'observa a l'atzar la puntuació màxima antrior. Aquesta estimació és una aproximació a la probabilitat de rebutjar erròniament la hipòtesi inicial de que el factor no s'uneix (p-value). Valors petits són indicatius de que la unió que identifiquem es difícil d'observar a l'atzar i, per tant, es raonable pensar que aquest FT s'uneix efectivament a la regió promotora. Aquest càlcul el farem de la següent forma:
1. generem una permutació dels nucleòtids de la regió promotora mitjançant el següent algorisme (conegut com a algorisme de Fisher-Yates):
```
        assumim tenim la sequencia promotora en un vector @v, el seguent
        algorisme permutara a l'atzar els elements de @v

        my $n = scalar(@v);
        my $i = $n - 1;
        while ($i >= 0) {
          my $j = int(rand($i+1));
          if ($i != $j) {
            my $tmp = $v[$i];

            $v[$i] = $v[$j];
            $v[$j] = $tmp;
          }
          $i = $i - 1;
        }
        
```
2. puntuem tots els llocs d'unió possibles al llarg de la seqüència permutada enregistrant el valor màxim observat
3. repetim aquests dos passos 100 cops, comptant en quants d'aquests casos la puntuació màxima observada és més gran o igual que s^*. Denotem aquest nombre de cops per c, direm que el p-value associat al FT és igual o més petit que c/100.

Cal tenir present que l'algorisme anterior és una aproximació simplificada al problema i, per tant, d'una capacitat predictiva limitada. Si voleu tenir una visió més real del problema d'identificar computacionalment llocs d'unió a FTs és aconsellable que llegiu els dos següents articles sobre el tema:

Wasserman WW, Sandelin A. Applied Bioinformatics for the identification of regulatory elements. Nat. Rev. Genetics, 5(4):276-87, 2004.

Tompa et al., Assessing computational tools for the discovery of transcription factor binding sites. Nat. Biotechnol., 23(1):137-44, 2005.