Bioinformàtica - 1er trimestre curs 2012/2013 - UPF
AGGACAGGTACGGCTGTCATCACTTAGACCTCACCCTGTGGAGCCACACCCTAGGGTTGG CCAATCTACTCCCAGGAGCAGGGAGGGCAGGAGCCAGGGCTGGGCATAAAAGTCAGGGCA GAGCCATCTATTGCTTACATTTGCTTCTGACACAACTGTGTTCACTAGCAACCTCAAACA GACACCATGGTGCACCTGACTCCTGAGGAGAAGTCTGCCGTTACTGCCCTGTGGGGCAAG GTGAACGTGGATGAAGTTGGTGGTGAGGCCCTGGGCAGGTTGGTATCAAGGTTACAAGAC AGGTTTAAGGAGACCAATAGAAACTGGGCATGTGGAGACAGAGAAGACTCTTGGGTTTCT GATAGGCACTGACTCTCTCTGCCTATTGGTCTATTTTCCCACCCTTAGGCTGCTGGTGGT CTACCCTTGGACCCAGAGGTTCTTTGAGTCCTTTGGGGATCTGTCCACTCCTGATGCTGT TATGGGCAACCCTAAGGTGAAGGCTCATGGCAAGAAAGTGCTCGGTGCCTTTAGTGATGG CCTGGCTCACCTGGACAACCTCAAGGGCACCTTTGCCACACTGAGTGAGCTGCACTGTGA CAAGCTGCACGTGGATCCTGAGAACTTCAGGGTGAGTCTATGGGACCCTTGATGTTTTCT TTCCCCTTCTTTTCTATGGTTAAGTTCATGTCATAGGAAGGGGAGAAGTAACAGGGTACA GTTTAGAATGGGAAACAGACGAATGATTGCATCAGTGTGGAAGTCTCAGGATCGTTTTAG TTTCTTTTATTTGCTGTTCATAACAATTGTTTTCTTTTGTTTAATTCTTGCTTTCTTTTT TTTTCTTCTCCGCAATTTTTACTATTATACTTAATGCCTTAACATTGTGTATAACAAAAG GAAATATCTCTGAGATACATTAAGTAACTTAAAAAAAAACTTTACACAGTCTGCCTAGTA CATTACTATTTGGAATATATGTGTGCTTATTTGCATATTCATAATCTCCCTACTTTATTT TCTTTTATTTTTAATTGATACATAATCATTATACATATTTATGGGTTAAAGTGTAATGTT TTAATATGTGTACACATATTGACCAAATCAGGGTAATTTTGCATTTGTAATTTTAAAAAA TGCTTTCTTCTTTTAATATACTTTTTTGTTTATCTTATTTCTAATACTTTCCCTAATCTC TTTCTTTCAGGGCAATAATGATACAATGTATCATGCCTCTTTGCACCATTCTAAAGAATA ACAGTGATAATTTCTGGGTTAAGGCAATAGCAATATTTCTGCATATAAATATTTCTGCAT ATAAATTGTAACTGATGTAAGAGGTTTCATATTGCTAATAGCAGCTACAATCCAGCTACC ATTCTGCTTTTATTTTATGGTTGGGATAAGGCTGGATTATTCTGAGTCCAAGCTAGGCCC TTTTGCTAATCATGTTCATACCTCTTATCTTCCTCCCACAGCTCCTGGGCAACGTGCTGG TCTGTGTGCTGGCCCATCACTTTGGCAAAGAATTCACCCCACCAGTGCAGGCTGCCTATC AGAAAGTGGTGGCTGGTGTGGCTAATGCCCTGGCCCACAAGTATCACTAAGCTCGCTTTC TTGCTGTCCAATTTCTATTAAAGGTTCCTTTGTTCCCTAAGTCCAACTACTAAACTGGGG GATATTATGAAGGGCCTTGAGCATCTGGATTCTGCCTAATAAAAAACATTTATTTTCATT GCAATGATGTATTTAAATTATTTCTGAATATTTTACTAAAAAGGGAATGTGGGAGGTCAG TGCATTTAAAACATAAAGAAATGAAGAGCTAGTTCAAACCTTGGGAAAATACACTATATC TTAAACTCCATGAAAGAAGGTGAGGCTGCAAACAGCTAATGCACATTGGCAACAGCCCTG ATGCCTATGCCTTATTCATCCCTCAGAAAAGGATTCAAGTAGAGGCTTGATTTGGAGGTTthe problems is to find the exonic structure of the genes encoded in this sequence, and to infer its amino acid sequence
To simplify we will assume that we know already that this sequence codes for a single complete gene in the forward strand.
We know that we can use a
PWM
to locate potential splice signals along the sequence. For instance,
for donor sites we could use a matrix such as ![]()
-3 -2 -1 +1 +2 +3 +4 +5 +6
A 0.34 0.87 -1.05 -inf -inf 0.71 1.06 -1.27 -0.46
C 0.33 -0.63 -2.22 -inf -inf -2.17 -1.19 -1.68 -0.38
G -0.30 -0.64 1.17 1.39 -inf 0.56 -0.72 1.20 -0.29
T -0.77 -0.59 -1.18 -inf 1.39 -2.29 -1.13 -1.58 0.66
where each coefficient ![]() is computed as
is computed as
![]() , where
, where ![]() is the probability of
nucleotide
is the probability of
nucleotide ![]() (
(
![]() ) at position
) at position ![]() in real donor
sites, and
in real donor
sites, and ![]() is the background probability of nucleotide
is the background probability of nucleotide ![]() .
.
This matrix can be used to score each potential donor site (GT),
along a given sequence.
The score of a potential donor site
![]() within the
sequence is computed as
within the
sequence is computed as
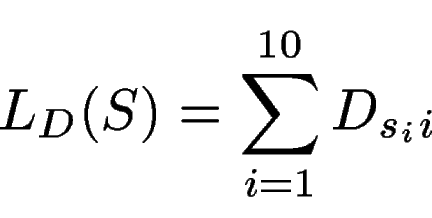 |
(1) |
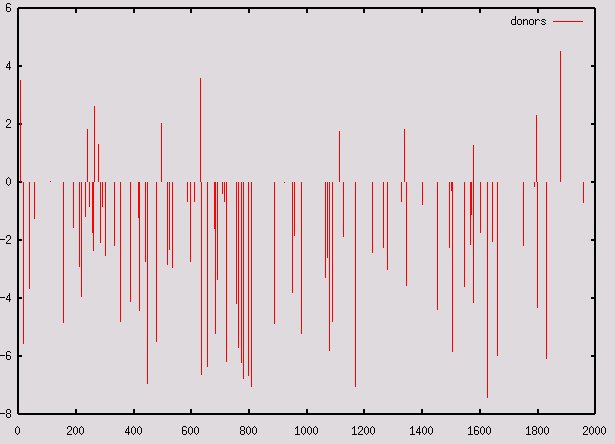
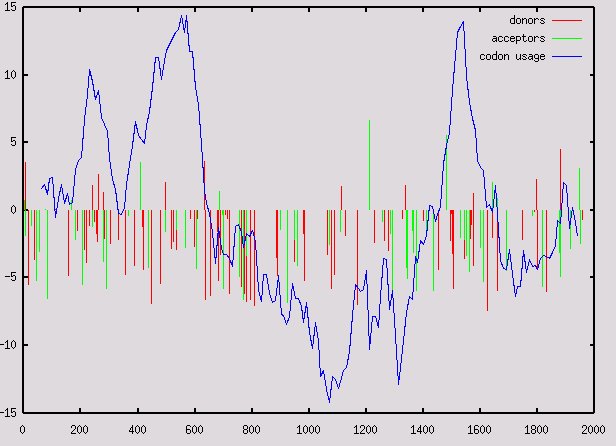
If we compute these scores along our sequence problem we would obtain something like:
We could simlarly compute the potential acceptor sites along the
sequence, ![]()
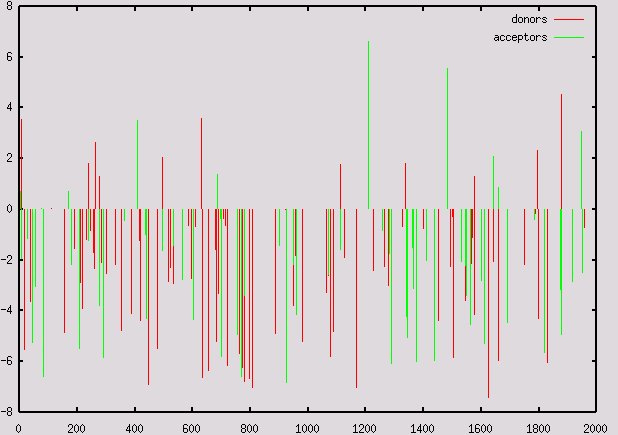
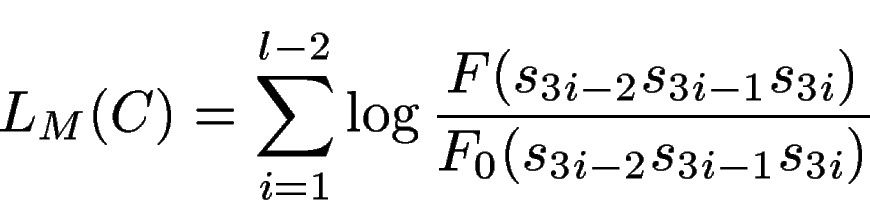
We can run an sliding window window along the query seqeunce above, and compute this log-likelihood ratio on each window. Below the plot obtained when the window size is 120 pb.
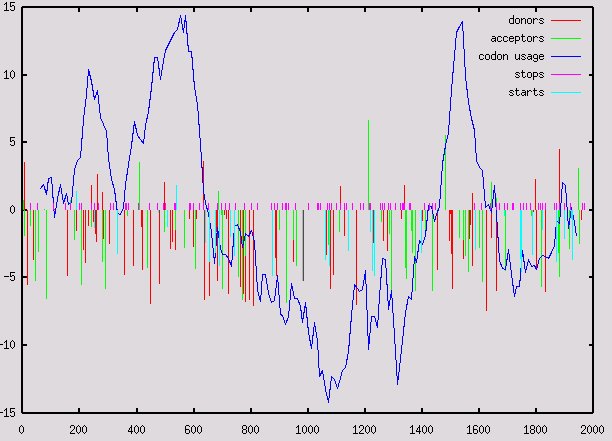
Actually to solve the gene prediction problem as stated above--infer the amino acid sequence of the encoded gene, we also need to locate potential start and stop codons. We can similarly built a PWM for start codons, because in around the codon ATG there is some conserved sequence context. There is no such context for stop codons. Thus, each TAA, TAG or TGA should be considered a potential stop codon.
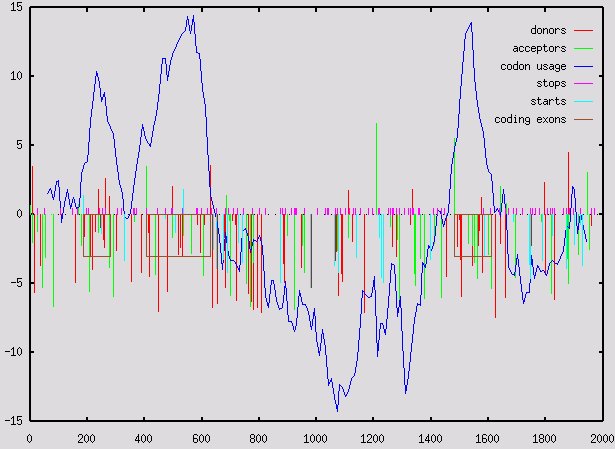
In one approach--that we call here ``exon-chaining approach''--, we just predict all potential exons that can be defined from the predicted splice signals, and score them according to the scores of the signals and of the codon bias in the exon sequence. Then, we just assemble the frame compatible chain of exons that maximizes the sum of the scores of the assembled exons.
The score of a potential exon, ![]() ,
, ![]() defined by sites
defined by sites
![]() (start/acceptor) and
(start/acceptor) and ![]() (donor/stop) is computed
as
(donor/stop) is computed
as
| (2) |

If a gene structure ![]() is a sequence of exons,
is a sequence of exons,
![]() , a natural
scoring function is
, a natural
scoring function is
| (3) |
The number of potential gene structures grows exponentially with the number of predicted exons, however a dynamic programming chaining algorithm that grows only linearly can be used to obtain the optimal solution.
| rguigo@imim.es |