Roderic Guigó, IMIM and UB, Barcelona

SEARCH BY SIGNAL

What is a motif?

Let A={A,C,G,T} be the alphabet of the nucleotide sequences. A motif (pattern, signal...) is an object dennoting a set of sequences on this alphabet, either in a deterministic or probabilistic way. Given a sequence S and a motif m, we will say that the motif m occurs in S if any of the sequences denoted by m occurs in S. We will use here indistinctly the terms motif, pattern, signal, etc. although these terms may be used with different meaning.

A Hierarchy of Motif Descriptors

Sequence motifs can be described in a wide variety of ways.

Exact Word

The simplest motif is just one string or sequence in the alphabet. The description is an specific sequence in the alphabet.

CTTAAAATAA

Exact words may encapsulate biologically functions, often when in the appropriate context. For instance, the sequence ``TAA'' denotes, under the appropriate circumstances, a translation stop codon.

Consensus Sequences

Often, however, biologically functions are carried out by related, but not identical, sequences. Usually these sequences can be aligned. For instance the sequences below

CTAAAAATAA
TTAAAAATAA
TTTAAAATAA
CTATAAATAA
TTATAAATAA
CTTAAAATAG
TTTAAAATAG
..........

are all are all known to bind the MEF2 (Myocyte enhancer factor 2) transcription factor. Sets of aligned sequences functionally related can be described by consensus sequences. The simplest form of a consensus sequence is obtained by picking the most frequent base at each position in the set of aligned sequences. More information on the underlying sequences can be captured by extending the alphabet with additional symbols, that allow to denote alternative possibilities to occur at a given position. For instance using the IUB (International Union of Biochemistry and Molecular Biology) nucleotide codes, the sequences above could be represented by the motif

YTWWAAATAR (Consensus MEF2 sequence, Yu et al., 1992)

were Y=[CT], W=[AT] and R=[AG]. MEF2 regulates genes specific to cardiac and skeletal muscle, such as Troponin Regular Expressions Regular expressions extend the alphabet further. Among the new symbols of this extended alphabet, there symbols dennoting the alternative occurence of a number of nucleotides at a given position, and symbols denoting that a given position may not be present. C..?[STA]..C[STA][^P]C 2Fe-2S ferredoxin, iron-sulfur binding region signature, PROSITE database, Bairoch, 1991) Other examples, DNA polymerase family B signature EF-hand calcium-binding domain This is an structural motif Position Weigth Matrices (PWMs) or Position Specific Scoring Matrices Information about the relative occurrence of each symbol at each position is lost in the motifs above. For instance in the alignment of MEF2 sites, both A and G are possible at the last position, but A appears in 5 sequences, while G appears only in two. This may reflect some underlying biological feature, for instance that the affinity of the binding is increased when Adenosine instead of Guanine appears at this position. We can capture explicitly this information by providing the relative frequency or probability of each symbol at each position along the alignment. These probabilities conform the so-called Position Weight Matrices (PWMs) or Position Specific Scoring Matrices (PSSMs). Follow the link for An Introduction to Position Weigth Matrices Examples of PWMs A PWM for donor sites. From a set of aligned donor sites we derive the following probability matrix -5 -4 -3 -2 -1 +1 +2 +3 +4 +5 +6 +7 +8 A 26.0 27.7 35.1 59.6 8.7 0.0 0.0 50.7 72.1 7.0 15.8 26.6 19.7 C 25.5 29.4 34.8 13.3 2.7 0.0 0.0 2.8 7.6 4.7 17.2 21.7 29.4 G 23.8 25.3 18.5 13.2 80.9 100.0 0.0 43.9 12.2 83.1 18.8 32.7 24.5 T 24.7 17.5 11.6 13.9 7.7 0.0 100.0 2.5 8.1 5.2 48.3 18.9 26.4 C/A A G G T A A G T which assuming nucleotide equiprobability tranforms in the following log-likelihood matrix: -5 -4 -3 -2 -1 +1 +2 +3 +4 +5 +6 +7 +8 A 0.04 0.10 0.34 0.87 -1.05 -inf -inf 0.71 1.06 -1.27 -0.46 0.06 -0.24 C 0.02 0.16 0.33 -0.63 -2.22 -inf -inf -2.17 -1.19 -1.68 -0.38 -0.14 0.16 G -0.05 0.01 -0.30 -0.64 1.17 1.39 -inf 0.56 -0.72 1.20 -0.29 0.27 -0.02 T -0.01 -0.36 -0.77 -0.59 -1.18 -inf 1.39 -2.29 -1.13 -1.58 0.66 -0.28 0.06 The positions showing higher bias in nucleotide composition are the most informative positions. 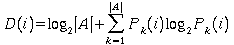Indeed, we can compute the information content at each position D(i), by using Shanon's formula where A is the alphabet {A, C, G, T} |A| is the number of elements in A, (A=4) P_k(i) is the probability of observing base k in position i so for a postion with nucleotide equiprobability P = 1/4, the information content is zero D(i) = 0 = 2 + 1/4 log₂(1/4) + 1/4 log₂(1/4) + 1/4 log₂(1/4) + 1/4 log₂(1/4) The information content along a sequence aligment can be nicely visualized by means of the so-called sequence logos. 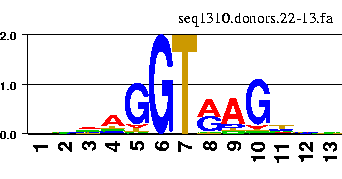There are a number of web servers that allow to generate the logos interactively. For instance the GENIO/logo server. You can try with the fasta file containing the aligment of above donor sites. The Jaspar database Modelling dependencies between positions In the case of the donor sites above, the matrix reproduces the complement to the sequence at the 5' end of the RNA molecule in the U1 snRNP, which interacts with the pre-mRNA sequence to recognize the donor site during the splicing process. This suggest that the recognition of the donor site is mediated by the formation of base pairs. The higher the complementariety between the precursor RNA molecule at the donor site and the 5' end of the U1 snRNP, higher the stability of the interaction. 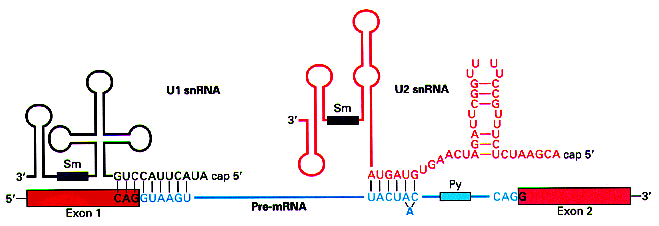(Figure taken from http://www.orst.edu/instruction/bb331/lecture10/lecture10.html) It is well known, however, that the staking energy contributes to the stability of the double stranded DNA. This staking energy depends on nearest neighbour arrengements along the DNA molecule. Tables of staking energy are constantly being updated. This suggest that the positions along the donor site sequence are not independent. That is, the existence of a given nucleotide at a given position may influence the probability of the nucleotides at the nearby positions. We can test this hypothesis by estimating the conditional probabilities of each nucleotide at each position, depending on the nucleotide at the precedent position, in the set above of known donor sites. position -3 position -2 position -1 position 1 position 2 position 3 position 4 position 5 position 6 A C G T A C G T A C G T A C G T A C G T A C G T A C G T A C G T A C G T A 29.2 31.9 25.5 13.4 62.4 9.5 15.2 12.9 7.0 1.7 86.2 5.1 0.0 0.0 100.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 65.4 9.5 13.3 11.8 6.0 3.0 87.4 3.7 19.1 15.9 39.8 25.3 C 48.6 32.5 6.2 12.7 69.2 11.6 6.4 12.8 19.1 7.1 55.2 18.5 0.0 0.0 100.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 72.7 4.7 6.7 16.0 19.5 17.8 42.8 20.0 24.8 25.2 10.6 39.4 G 38.8 36.2 17.7 7.3 62.6 15.8 12.3 9.3 12.3 2.4 79.1 6.2 0.0 0.0 100.0 0.0 0.0 0.0 0.0 100.0 0.0 0.0 0.0 0.0 82.5 5.6 9.0 2.9 6.2 4.2 86.1 3.4 15.2 17.2 15.9 51.7 T 16.4 41.3 29.5 12.9 17.7 25.6 29.5 27.2 2.9 3.3 84.4 9.4 0.0 0.0 100.0 0.0 0.0 0.0 0.0 0.0 50.8 2.8 43.8 2.5 26.9 7.5 50.7 14.9 6.1 7.9 78.7 7.2 12.5 10.7 43.4 33.5 35.1 34.8 18.5 11.6 59.6 13.3 13.2 13.9 8.7 2.7 80.9 7.7 0.0 0.0 100.0 0.0 0.0 0.0 0.0 100.0 50.7 2.8 43.9 2.5 72.1 7.6 12.2 8.1 7.0 4.7 83.1 5.2 15.8 17.2 18.8 48.3 we can use this conditional probability distribution to compute the probabilyt of a given sequence in a donor site. The probability of sequence S=s1s2s3s4s5s6s7s8s9 in a donor site can be computed now as P(S)=P(s1) P(s2/s1) P(s3/s2) P(s4/s3) P(s5/s4) P(s6/s5) P(s7/s6) P(s8/s7) P(s9/s8) where P(si/sj) is the probability of nucleotide sj in position k given that nucleotides si is at position k-1. For instance, the probability of finding sequence S=CAGGTTGGA is P(S)= 0.35 * 0.69 * 0.55 * 1.00 * 1.00 * 0.02 * 0.51 * 0.86 * 0.15 Actually, we usually compute a log-likelihood ratio as above. Assuming for instance p(si/sj)=0.25 ---that is, that there is no dependence between positions, we obtain the following log-likelihood matrix position -3 position -2 position -1 position 1 position 2 position 3 position 4 position 5 position 6 A C G T A C G T A C G T A C G T A C G T A C G T A C G T A C G T A C G T A 0.15 0.24 0.02 -0.62 0.91 -0.97 -0.50 -0.66 -1.28 -2.72 1.24 -1.58 -inf -inf 1.39 -inf -inf -inf -inf -inf -inf -inf -inf -inf 0.96 -0.97 -0.63 -0.75 -1.43 -2.12 1.25 -1.92 -0.27 -0.46 0.46 0.01 C 0.66 0.26 -1.40 -0.67 1.02 -0.76 -1.37 -0.67 -0.27 -1.25 0.79 -0.30 -inf -inf 1.39 -inf -inf -inf -inf -inf -inf -inf -inf -inf 1.07 -1.68 -1.32 -0.45 -0.25 -0.34 0.54 -0.22 -0.01 0.01 -0.86 0.46 G 0.44 0.37 -0.35 -1.24 0.92 -0.46 -0.71 -0.99 -0.71 -2.33 1.15 -1.40 -inf -inf 1.39 -inf -inf -inf -inf 1.39 -inf -inf -inf -inf 1.19 -1.50 -1.02 -2.16 -1.39 -1.78 1.24 -1.99 -0.50 -0.37 -0.45 0.73 T -0.42 0.50 0.16 -0.66 -0.35 0.02 0.17 0.08 -2.16 -2.03 1.22 -0.97 -inf -inf 1.39 -inf -inf -inf -inf -inf 0.71 -2.17 0.56 -2.29 0.07 -1.21 0.71 -0.52 -1.41 -1.15 1.15 -1.24 -0.69 -0.85 0.55 0.29 0.34 0.33 -0.30 -0.77 0.87 -0.63 -0.64 -0.59 -1.05 -2.22 1.17 -1.18 -inf -inf 1.39 -inf -inf -inf -inf 1.39 0.71 -2.17 0.56 -2.29 1.06 -1.19 -0.72 -1.13 -1.27 -1.68 1.20 -1.58 -0.46 -0.38 -0.29 0.66 PRACTICAL OTHER PRACTICALS PRACTICAL 1 PRACTICAL 2 PRACTICAL 3