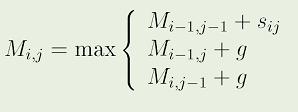
On Mi,j = Posició de la matriu que estem calculant
Mi-1,j-1 + Sij= alineament dels dos residus
Mi-1,j + g = alinear el residu horitzontal amb un gap
Mi,j-1 + g = alinear el residu vertical amb un gap
La programació dinàmica és un mètode computacional empreat per alinear dues proteïnes o cadenes d'àcids nucleics.
De forma metafòrica podriem dir que l'algorisme de programació dinàmica és com els camins per anar a Roma, aquests són multiples, però poden ser més o menys llargs. Aquest algoristme ens permetrà obtenir doncs aquell camí òptim per arribar-hi disminuint el nombre de càlculs necesaris. Per aplicar l'algoristme de programació dinàmica hem de fer una matriu amb les dues seqüències; i aplicar de forma recurrent el següent càlcul:
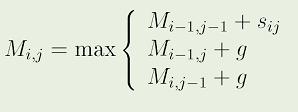
On Mi,j = Posició de la matriu que estem calculant
Mi-1,j-1 + Sij= alineament dels dos residus
Mi-1,j + g = alinear el residu horitzontal amb un gap
Mi,j-1 + g = alinear el residu vertical amb un gap
La penalització que s'aplica per l'ús del gap no és sempre constant,ja que existeix una penalització per la opertura de gap i per la seva extensió.
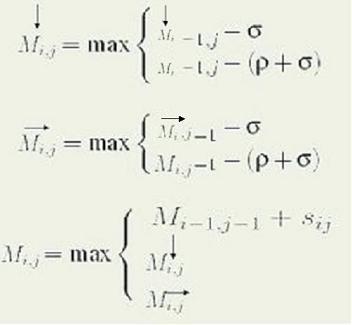
En l'última clau es representa exactament el mateix que la figura anterior. Pot ser que tinguem alineament
(representat per la lletra delta) o potser que tinguem un gap en alguna de les dues seqüències.
En la primera clau apareix l'ús del gap en la primera seqüència. Pot ser que al colocar un gap en la posició Mi,j
simplement sigui una extensió d'un gap preexistent(sigma)o bé pot ser que hi hagi opertura i extensió d'aquest(sigma + ro).
La segona clau representa exactament el mateix que la primera però quan el gap es troba a la segona seqüència.
Al alinear dues seqüències ens podem trobar davant de dues situacions diferents. En primer lloc pot ser que la posició contingui el mateix residu, amb la qual cosa tindriem una correspondència exacta o bé que siguin diferents,observant doncs una correspondencia inexacte.
Com que trobar l'alineament perfecte es impossible, ens quedarem amb el millor dels alineaments aconseguits amb el esquema de puntuacions que haguem assignat. Aquest es coneix com alineament òptim.
Un gap és una posició en blanc en l'alineament de dues seqüències degut a un procés de inserció o delecció d'algun residu en alguna de les seqüències. El fet d'afegir gaps als alineaments suposa una penalització en la seva puntuació, per això es important evitar els alineaments amb múltiples gaps.
La penalització que s'aplica és per a:
Les matrius de substitució o taules de comparació de simbols ens permeten comptar quantes vegades observem un canvi d'aminoàcid per un altre. Les matrius de puntuació són l'element que ens permet assignar una puntuació durant l'emparellament dels diferents aminoàcids.
Al igual que existeixen matrius de substitució per a aminoàcids també les trobem per a nucleotids. Existeixen dos tipus principals de matrius de substitució:
Les matrius PAM (Point Accepted Mutations) són matrius de puntuació per a l'alineament de cadenes peptídiques elaborada per Margaret Oakley Dayhoff i el seu equip de colaboradors a la National Biomedical Research Foundation (NBRF) als EUA. Aquest grup va ser el primer en crear una col·lecció de seqüències de proteïnes les quals van recollir al Atlas of Proteïn Sequence and Structure.

Aquestes col·leccions de proteïnes van permetre posteriorment l'aparició de les primeres bases de dades. Dayhoff i els seus colaboradors van classificar aquestes proteïnes en families i superfamilies tenint en compte el grau de semblança que presentaven. Un cop classificades aquestes proteïnes van obtenir les matrius PAM atenent a les 1572 substitucions detectades en aquests 71 grups de seqüències de proteïnes amb un 85% d'homologia.Degut a que els canvis observats són entre proteïnes estretament relacionades, aquests canvis representen substitucions d'aminoàcids que no canvieen de forma significativa la funció de la proteïna. Es per això que Dayhoff va anomenar-les mutacions acceptades. Aquestes són definides com a canvis aminoacidics acceptats per la selecció natural.
Les matrius PAM estan basades per tant en l'alineament global de proteïnes estretament relacionades.
No hi ha cap altre tipus de matriu de puntuació que estigui basat en aquests canvis evolutius. El model evolutiu en que es basen assumeix que les substitucions dels residus observades en un periode breu de temps poden ser extrapolades cap a períodes de temps més grans.
La primera matriu PAM que es va fer va ser la PAM1 la qual conté els resultats de comparar seqüències que tenen una divergència igual al 1%.
Per obtenir els valors de la taula es van contar el nombre de vegades que un determinat aminoàcid mutava a un altre. Llavors per a corretgir els errors provocats per variacions en la composició de les proteïnes(abundància de determinats aa en fornt d'altres , taxes de mutació dels aa i longituds de les seqüències analitzades es va dividir el nombre de canvis en la seqüència entre el factor d'exposició del aa. Aquest paràmetre s'obté dividint la abundància dels aa entre els canvis d'aminoàcids comptabilitzats entre el grup de seqüències per cada 100 posicions.
La resta de matrius PAM s'extrapolen a partir de la matriu PAM1. El nombre que acompanya les matrius PAM indica la distància evolutiva. Atenent això si el que volem es alinear dues seqüències allunyades evolutivament ens interesa fer una matriu PAM amb un numero elevat, mentre que per alinear seqüències properes caldrà fer servir matrius PAM amb valors baixos.
Les matrius BLOSUM són posteriors a les matrius PAM. A diferencia d'aquestes no estan basades en cap model evolutiu i s'elaboren a partir de l'observació de canvis en una sèrie de patrons d'aa conservats anomenats blocs.
Les matrius BLOSUM estan basades en aliniament local, i no en global com ho estan les matrius PAM. Una de les matrius BLOUSUM més usades és la BLOSUM62. Aquest valor que acompanya a la matriu ens indica el mínim percentatge d'identitat dels blocs per construir la matriu, en el cas de BLOSUM62 les seqüències tenen una similaritat mínima del 62%. Una diferència important d'aquestes matrius respecte les PAM és que no estan extrapolades, sinó que els seus valors estan recalculats per a cada percentatge mínim de identitat.
Exemple de matriu BLOSUM62:
# Matrix made by matblas from blosum62.iij # * column uses minimum score # BLOSUM Clustered Scoring Matrix in 1/2 Bit Units # Blocks Database = /data/blocks_5.0/blocks.dat # Cluster Percentage: >= 62 # Entropy = 0.6979, Expected = -0.5209 A R N D C Q E G H I L K M F P S T W Y V * 4 -1 -2 -2 0 -1 -1 0 -2 -1 -1 -1 -1 -2 -1 1 0 -3 -2 0 -4 -1 5 0 -2 -3 1 0 -2 0 -3 -2 2 -1 -3 -2 -1 -1 -3 -2 -3 -4 -2 0 6 1 -3 0 0 0 1 -3 -3 0 -2 -3 -2 1 0 -4 -2 -3 -4 -2 -2 1 6 -3 0 2 -1 -1 -3 -4 -1 -3 -3 -1 0 -1 -4 -3 -3 -4 0 -3 -3 -3 9 -3 -4 -3 -3 -1 -1 -3 -1 -2 -3 -1 -1 -2 -2 -1 -4 -1 1 0 0 -3 5 2 -2 0 -3 -2 1 0 -3 -1 0 -1 -2 -1 -2 -4 -1 0 0 2 -4 2 5 -2 0 -3 -3 1 -2 -3 -1 0 -1 -3 -2 -2 -4 0 -2 0 -1 -3 -2 -2 6 -2 -4 -4 -2 -3 -3 -2 0 -2 -2 -3 -3 -4 -2 0 1 -1 -3 0 0 -2 8 -3 -3 -1 -2 -1 -2 -1 -2 -2 2 -3 -4 -1 -3 -3 -3 -1 -3 -3 -4 -3 4 2 -3 1 0 -3 -2 -1 -3 -1 3 -4 -1 -2 -3 -4 -1 -2 -3 -4 -3 2 4 -2 2 0 -3 -2 -1 -2 -1 1 -4 -1 2 0 -1 -3 1 1 -2 -1 -3 -2 5 -1 -3 -1 0 -1 -3 -2 -2 -4 -1 -1 -2 -3 -1 0 -2 -3 -2 1 2 -1 5 0 -2 -1 -1 -1 -1 1 -4 -2 -3 -3 -3 -2 -3 -3 -3 -1 0 0 -3 0 6 -4 -2 -2 1 3 -1 -4 -1 -2 -2 -1 -3 -1 -1 -2 -2 -3 -3 -1 -2 -4 7 -1 -1 -4 -3 -2 -4 1 -1 1 0 -1 0 0 0 -1 -2 -2 0 -1 -2 -1 4 1 -3 -2 -2 -4 0 -1 0 -1 -1 -1 -1 -2 -2 -1 -1 -1 -1 -2 -1 1 5 -2 -2 0 -4 -3 -3 -4 -4 -2 -2 -3 -2 -2 -3 -2 -3 -1 1 -4 -3 -2 11 2 -3 -4 -2 -2 -2 -3 -2 -1 -2 -3 2 -1 -1 -2 -1 3 -3 -2 -2 2 7 -1 -4 0 -3 -3 -3 -1 -2 -2 -3 -3 3 1 -2 1 -1 -2 -2 0 -3 -1 4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 1